news
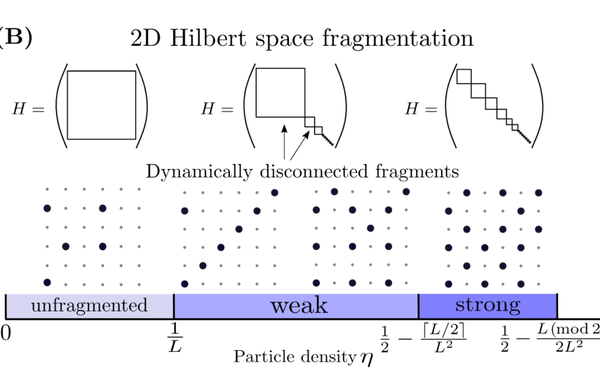
Quantum hard disks on a lattice
Machine learning solves complex quantum problems
Due to a new method, artificial neural networks, as used in machine learning, will be able to be trained quicker so as to be able to solve complex problems in quantum mechanics. For example, previously unexplained properties of a special state of matter, the quantum spin liquid, can be calculated, something that has not been possible with any previous method to date. This has been made possible by a new optimisation method developed by the Institute of Physics.

Honorary doctorate for Prof. Dieter Vollhardt
Prof. Dieter Vollhardt was awarded an honorary doctorate by the 威尼斯赌博游戏_威尼斯赌博app-【官网】 of Warsaw last week in recognition of his scientific achievements and longstanding collaboration with theoretical physicists at the 威尼斯赌博游戏_威尼斯赌博app-【官网】 of Warsaw.

Leading quantum mechanical research
The Centre for Electronic Correlations and Magnetism (EKM) was established in the early 1990s. Since then, it has become a top research institute in the field of quantum mechanics. The meeting of the scientific advisory board of the EKM in Augsburg, composed of leading experts in the field, confirms this.

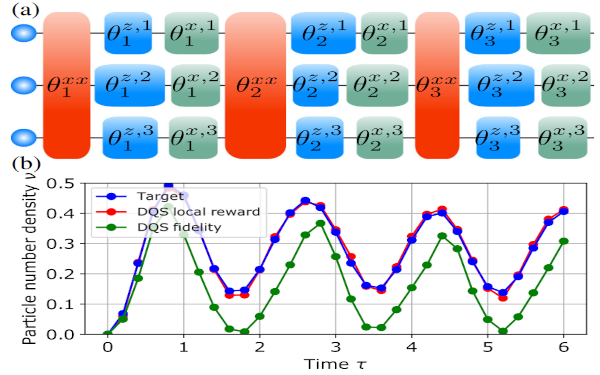
Paper: Reinforcement Learning for Digital Quantum Simulation
Digital quantum simulation on quantum computers provides the potential to simulate the unitary evolution of any many-body Hamiltonian with bounded spectrum by discretizing the time evolution operator through a sequence of elementary quantum gates. A fundamental challenge in this context originates from experimental imperfections, which critically limits the number of attainable gates...
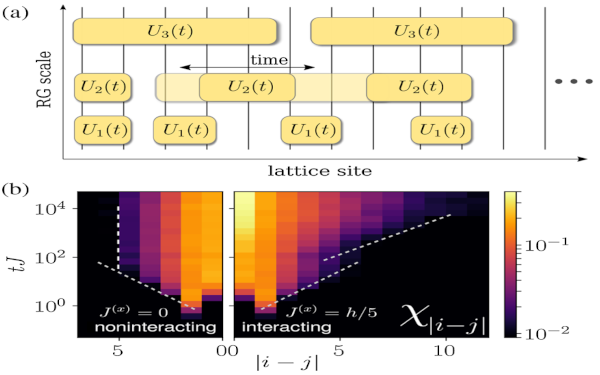
Paper: Unitary Long-Time Evolution with Quantum Renormalization Groups and Artificial Neural Networks
In this work, we combine quantum renormalization group approaches with deep artificial neural networks for the description of the real-time evolution in strongly disordered quantum matter. We find that this allows us to accurately compute the long-time coherent dynamics of large many-body localized systems in nonperturbative regimes including the effects of many-body resonances.
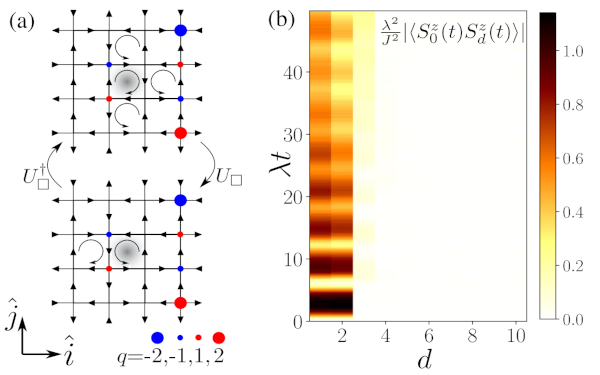
Paper: Disorder-Free Localization in an Interacting 2D Lattice Gauge Theory
Disorder-free localization has been recently introduced as a mechanism for ergodicity breaking in low-dimensional homogeneous lattice gauge theories caused by local constraints imposed by gauge invariance. We show that also genuinely interacting systems in two spatial dimensions can become nonergodic as a consequence of this mechanism.